A note on fractional dilution

(09 May 2023) notes

I’ve been working on extending the capabilities of the eVOLVER system. The eVOLVER is an open source platform with 16 reactor sleeves with individual control of temperature, stir rates and media flow rates into each reactor.

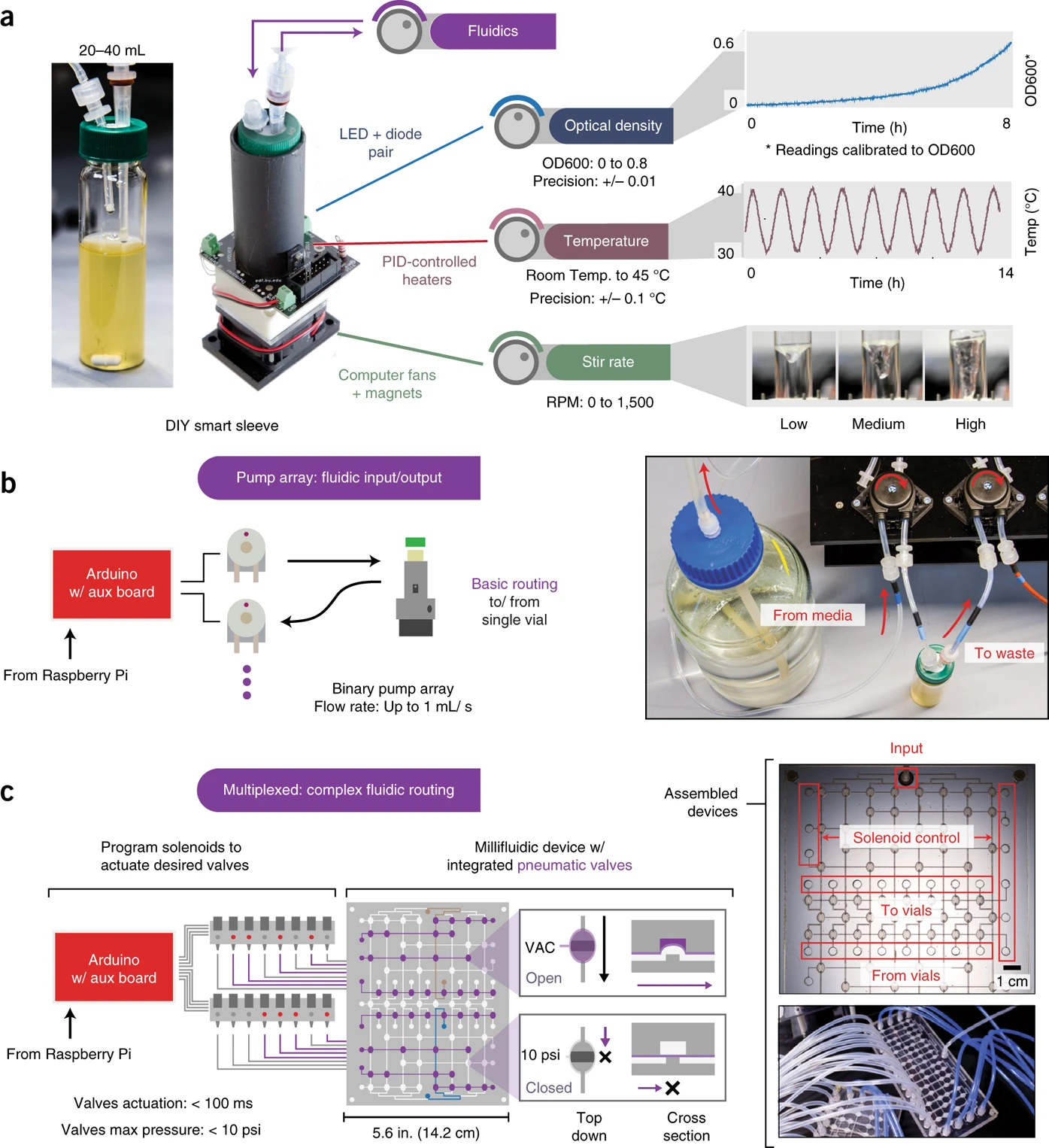
Figure 2 from Wong et al 2018, Nature Biotech. They don't in fact measure OD600 as this figure would have you believe.

While attempting to improve the quality of OD measurements, we recognized that the main source of noise in these measurements came from the glass vial itself. One solution to this problem is to redo an OD calibration in the glass vial directly. I propose to do this by starting with a dense culture, and sequentially adding a fixed bolus of media until we span the OD range that we are interested in. By recording the sensor values (there are two sensors that record the scattering of 900nm light through the culture) at each dilution step, we can use this calibration data to then infer real ODs during an experiment.

The Proposal

If I dispense a fixed bolus of media and record the sensor readings, I’ll be able to construct a calibration curve. Here is an example of the outcome of this calibration, with the red dots being the sensor readings at each dilution curve, and the colored dots representing the timecourse, with bright colors representing later times.

$Left: An illustration of the fractional dilution scheme with repeated additions of a fixed bolus of media to a dense culture. Right: An example of a successful calibration, the axes show the sensor readings, and the red points show readings at discrete dilution events$

The Problem

Given a 20mL culture at OD 1, I need to dilute this down to an OD of 0.01 in the vial. How much media do I need?

If vial volume wasn’t a constraint, per c1 v1 = c2 v2, I’ll need 20mL*(1/0.01) ≅ 2000mL per vial ! That would mean, for 16 vials, I’d need about 32L of media which is ridiculous.

Stepping back a second, I didn’t actually do this calculation when I was testing out the dilution strategy. I just went ahead and dispensed a fixed “bolus” into each vial. The first time I add the bolus, the effective dilution is

$c_{\text{first dilution}} = c_{\text{initial}} \frac{V}{V + bolus}$.

I then aspirate off the bolus volume, so the total volume is again V.

The second time I do it, it becomes

$c_{\text{second dilution}} = c_{\text{first dilution}} \frac{V}{V + bolus} = c_{\text{initial}} \left(\frac{V}{V + bolus}\right)^2$.

At the end of $n$ steps, my final concentration is

\[c_n = c_{\text{initial}}\left(\frac{V}{V + bolus}\right)^n\]

For a volume V going from startOD to endOD with additions of bolusmL media at each step, I calculated that I’d need n dilution steps, where

\[n = \frac{\log(endOD/startOD)}{\log(V/(V + bolus))}\]

I noticed that I always needed far less than the predicted 32L of media for a 100X dilution. In fact, it was always less than 2L for all 16 vials put together. Was I doing something wrong? How was I so efficiently diluting over 2 orders of magnitude with such a small total volume of media?

The Theory

So what was the total cumulative volume being consumed in my calibration procedure? Well, for the fixed bolus size, it was as simple as

\[V_{\text{cumulative}} = n \text{bolus} = \text{bolus} \frac{\log(endOD/startOD)}{\log(V/(V + \text{bolus}))}\]

That didn’t mean much to me, so I plotted it out.

How does the cumulative volume dispensed change with different bolus sizes dispensed?

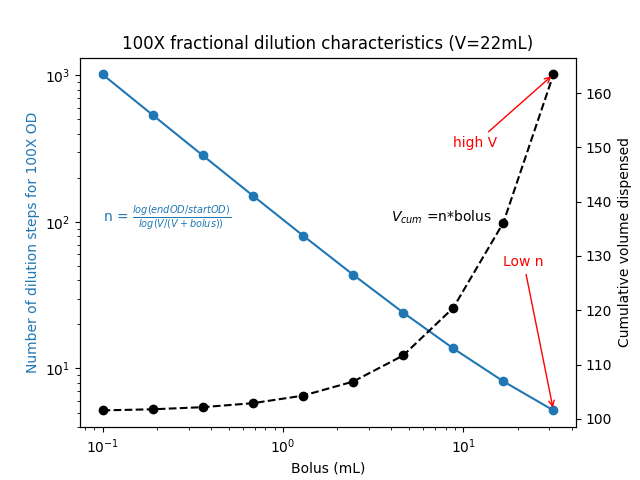
Variation of number of dilution steps (left) and total volume dispensed (right) with bolus size for a volume of 22mL over a 100X dilution range.

Two observations stood out to me.

At large bolus sizes, the number of dilution steps needed went down. This makes sense.
As the bolus size decreased, the total volume dispensed seemed asymptotically reach a lower limit. Huh?

So I decided to calculate the $\text{lim}_{\text{bolus}\rightarrow 0} V_{\text{cumulative}}$.

\[\text{lim}_{\text{bolus}\rightarrow 0} \text{bolus} \frac{\log(endOD/startOD)}{\log(V/(V + \text{bolus}))}\]

I’d forgotten how to solve this limit when things were going to zero in the numerator and denominator. Sushrut Karmalkar reminded me to apply l’Hopital’s rule and differentiate the two parts

Numerator: $\frac{d}{d \text{bolus}}\text{bolus} \log(endOD/startOD) = \log(endOD/startOD)$

Denominator: $\frac{d}{d \text{bolus}} \log(V/(V + \text{bolus})) = \frac{1}{V/(V+bolus)} \frac{-V}{(V+bolus)^2} = \frac{-1}{(V+bolus)} = \frac{-1}{V}$ as bolus goes to zero.

Putting this together:

\[\text{lim}_{\text{bolus}\rightarrow 0} V_{\text{cumulative}}= -V \log\frac{endOD}{startOD} = \boxed{V \log \frac{startOD}{endOD}}\]

This was pretty cool! So over a 100X dilution for a volume of 22mL, I’d only need about 22ln(100) = 22*4.6 = 101.9 mL! Nowhere close to the 2L if I was to do the entire dilution in a single step.

What did I just read

I’ve been scratching my head about this one for a few days now. This seems to be a general result in fractional dilution systems. I immediately thought of fractional killing in chemotherapy, or multiple doses of antibiotics. The intuition for these systems is always that we are killing off a fixed fraction of cancer cells/pathogens at each dose. But the result above indicates that repeated doses allows for a reduction of the total amount of therapeutic used as well! This is pretty cool.

I looked around briefly for other domains where this law comes up. The only other thing I’ve been able to find is what is called the Basic Room Purge Equation which states that in order to reduce the concentration of a particular gas say carbon monoxide in a room, the time required at a flow rate of clean air Q in a room of volume V is

\[D_t = \frac{V}{Q}\log \frac{C_i}{C_f}\]

Very interesting.

Moral of the story

I continue to be convinced that I don’t have a strong intuition for fractions.
This fractional dilution law definitely has a lot of applications. Let me know if this has been discussed at length somewhere!