Compartmental model of cytoskeletal polarization during chemotaxis
This blog post summarizes the class project that I did with @boribong this semester. We created a phenomenological model of neutrophil polarization during chemotaxis, a straightforward attempt where we compartmentalized a cell radially to to simulate the heterogeneous cytoskeletal reorganization. Check out this cool animation that I made! F-actin polymerization in red, myosin contraction activity in Blog post coming soon!
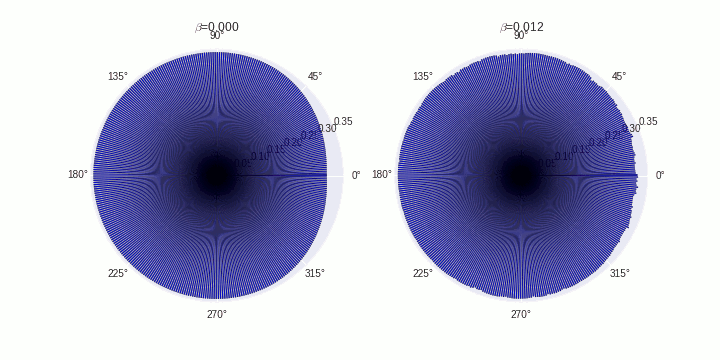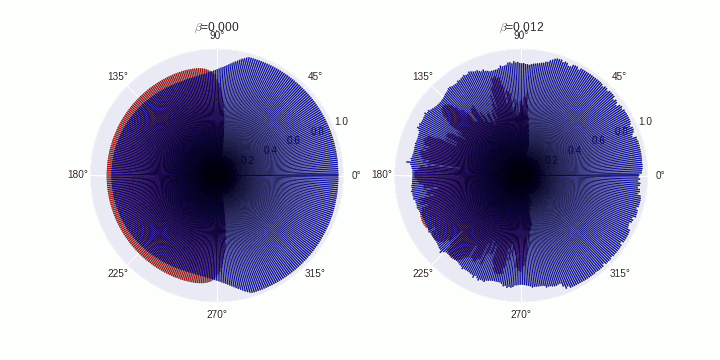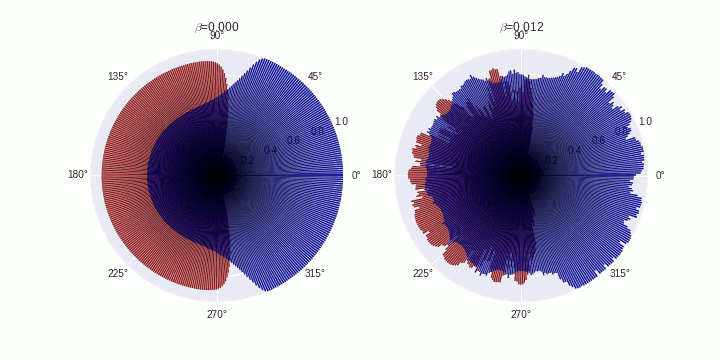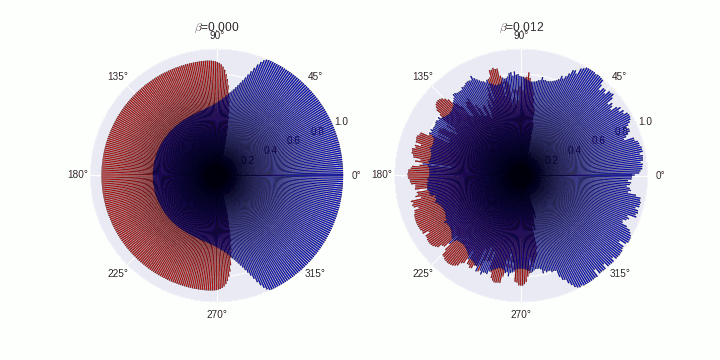
This is my first attempt at creating a blog post directly from my jupyter notebook. Here goes! :)
Incorporating network structure into coupled cytoskeletal network
Headers and functions
%matplotlib inline
import matplotlib.pyplot as plt
import PyDSTool as dst
import numpy as np
import numpy.random as random
import seaborn as sns
import matplotlib.cm as cm
from matplotlib.pyplot import figure, show, rc
import networkx as nx
import pandas as pd
from tqdm import tqdm
import pickle
plt.rcParams['figure.figsize']=10,5
def makeheatmap(string,pointset):
pts=pointset
col=[]
mat=[]
for j in range(0,len(pts[string+'0'])):
for i in range(0, COMPARTMENTS):
col.append(pts[string+str(i)][j])
mat.append(col)
col=[]
mat.reverse()
#mat.transpose()
fig,ax=plt.subplots()
ax=sns.heatmap(mat,cmap="YlGnBu")
def initialLdist(COMPARTMENTS,maxL,s):
x=np.linspace(0,2.0,COMPARTMENTS+1)
L=[]
for i in range(0,len(x)):
L.append(maxL*np.exp(-((x[i]-1.0)/s)**2))
return L
def actindefinition(edgelist):
A=edgelist
vardict={}
for n in A.keys():
ASSIGNMENT="gamma_actin*(shs(S,kactin*RacGTP"+n+"-k_actin_degr*"
numNeigh=len(A[n])
ASSIGNMENT=ASSIGNMENT+"("+str(numNeigh)+"*Actin"+n
for nei in A[n]:
ASSIGNMENT=ASSIGNMENT+"-Actin"+nei
ASSIGNMENT=ASSIGNMENT+"+w_actin))-Actin"+n+")"
vardict['Actin'+n]=ASSIGNMENT
return vardict
def myosindefinition(edgelist):
A=edgelist
vardict={}
for n in A.keys():
ASSIGNMENT="shs(S,kmyosin*RhoA"+n+"-k_degr_myosin*"
numNeigh=len(A[n])
ASSIGNMENT=ASSIGNMENT+"("+str(numNeigh)+"*Myosin"+n
for nei in A[n]:
ASSIGNMENT=ASSIGNMENT+"-Myosin"+nei
ASSIGNMENT=ASSIGNMENT+"))-Myosin"+n
vardict['Myosin'+n]=ASSIGNMENT
return vardict
Watts-Strogatz randomization
# Generating random graphs
N=360
K=4
n=N #int(raw_input('Please enter number of nodes in graph: ') or "10")
if n<=0:
sys.exit('n has to be positive!')
nodelist=np.arange(0,n)
k=K #int(raw_input('Please enter average degree of each node.\nFor n=%i, enter an even integer between 1 and n: ' % n) or '2')
if k%2 !=0:
sys.exit('k is not even!')
if k >n:
sys.exit('k is too large!')
degreecount=np.arange(-k/2,(k+2)/2)
G=nx.Graph()
for i in range(0,len(nodelist)):
for j in range(0,len(degreecount)):
if i+degreecount[j]>n-1:
G.add_edge(str(nodelist[i]),str(nodelist[i+degreecount[j]-n-1]))
#print i,"\t",j,"\t",nodelist[i],nodelist[i+degreecount[j]-n-1]
else:
if nodelist[i+degreecount[j]]!=nodelist[i]:
G.add_edge(str(nodelist[i]),str(nodelist[i+degreecount[j]]))
#f.close()
for node in G.nodes():
if node in G.neighbors(node):
G.remove_edge(node,node)
print "removed an edge"
def rewire(H,p):
#Function takes in a graph and a probability p, and returns average shortest path length and average clustering coefficient of the rewired graph
nodeset=set(H.nodes())
for node in H.nodes(): #rewiring
neighborset=set(H.neighbors(node))
targetlist=list(nodeset-neighborset)
for tailnode in H.neighbors(node):
r=random.random()
if r<p:
node_selection=random.randint(0,len(targetlist)-1)
H.remove_edge(node,tailnode)
H.add_edge(node,targetlist[node_selection])
#asp=[]
return H
def generate_adlist(G):
node=G.nodes()
neighbors={}
for e in G.edges():
for n in node:
neighbors[n]=G.neighbors(n)
return neighbors
removed an edge
Generate and store adjacency lists for rewired graphs
beta=list(np.logspace(-3.0,-1.56,5)) # Specify probabilities of rewiring
#P=[0.01]
beta.insert(0,0.0)
Adict=[]
for b in beta:
A={}
graph=rewire(G.copy(),b)
# graph=graph.to_undirected()
# graph=rewire(G,0.15)
A=generate_adlist(graph)
Adict.append(A)
#B=generate_adlist(G)
Model definition
COMPARTMENTS=N-1
RevisedCompArgs=dst.args(name='small-world-cyto',
varspecs={
# input set to constant initial value by default
'L[i]':'for(i,0,'+str(COMPARTMENTS)+',0)',#kp-klr*L[i]*R[i]-kd)',
'PIP[i]':'for(i,0,'+str(COMPARTMENTS)+',gamma_pip*(shs(S,wlr*L[i]*R[i]-wpip)-PIP[i]))',
# Regulators
'RacGTP[i]':"for(i,0,"+str(COMPARTMENTS)+",shs(S,-w_rac_rac*RacGTP[i]+w_rac_pip*PIP[i])-RacGTP[i])",
'RhoA[i]':"for(i,0,"+str(COMPARTMENTS)+",(shs(S,wlr_rho*L[i]*R[i]-w_actin_rho*Actin[i])-RhoA[i]))",
},
pars={
# PIP Parameters
'wpip':0.45,
'gamma_pip':0.5,
'wlr':1.0,
# RacGTP activation
'w_rac_pip':3.0,
# Rac
'w_rac_rac':1.5,
# Rho
'w_actin_rho':6.0,
'wlr_rho':1.0,
'S':10,
'kactin':1.0,#0.1,
'w_actin':0.77,
'k_actin_degr':1.0,
'gamma_actin':10.0,
'kmyosin':1.0,
'k_degr_myosin':10
},
ics={
},
fnspecs={
'shs':(['sig','summ'],'1.0/(1.0+exp(-sig*summ))'),
'actinweight':(['n','denom'],'n/denom')
},
tdata=[0,20]
)
SimData=[]
for A in tqdm(Adict):
act=[]
RevisedCompArgs.varspecs.update(actindefinition(A))
RevisedCompArgs.varspecs.update(myosindefinition(A))
# RevisedCompArgs.varspecs.update(actindefinition(B))
# RevisedCompArgs.varspecs.update(myosindefinition(B))
#s=[0.1,0.3,0.5,0.7,0.9,1.1,1.3,1.5]
s=[0.5]
AMRatio=[]
#for v in s:
L=initialLdist(COMPARTMENTS,1.5,s)
Rinitial=1.0
PIPinitial=0.0
Racinitial=0.0
Actininital=0.0
Rhoinitial=0.0
Myosininitial=0.0
for i in range(0,COMPARTMENTS+1):
R=str('R'+str(i))
RevisedCompArgs.pars[R]=Rinitial
PIP=str('PIP'+str(i))
RevisedCompArgs.ics[PIP]=PIPinitial
Rac=str('RacGTP'+str(i))
RevisedCompArgs.ics[Rac]=Racinitial
Actin=str('Actin'+str(i))
RevisedCompArgs.ics[Actin]=Actininital
Rho=str('RhoA'+str(i))
RevisedCompArgs.ics[Rho]=Rhoinitial
Myosin=str('Myosin'+str(i))
RevisedCompArgs.ics[Myosin]=Myosininitial
Lval=str('L'+str(i))
RevisedCompArgs.ics[Lval]=L[i]
RevisedCompDS=dst.Vode_ODEsystem(RevisedCompArgs)
pts=RevisedCompDS.compute('test').sample(dt=0.5)
SimData.append(pts)
len(SimData)
6
# Example of makeheatmap() usage
makeheatmap('Myosin',SimData[0])

def minmaxglobal(Llist):
maxglob=[]
minglob=[]
for L in Llist:
maxglob.append(max(L))
minglob.append(min(L))
mini=min(minglob)
maxi=max(maxglob)
normllist=[]
normlist=[]
for i in range(0,len(Llist)):
normlist=[]
for j in range(0,len(Llist[i])):
normlist.append((Llist[i][j]-mini)/(maxi-mini))
normllist.append(normlist)
return normllist
f=figure(figsize=(8,8))
ax=f.add_axes([0.1, 0.1, 0.8, 0.8],polar=True)
theta = np.linspace(0.0, 2.0*np.pi, 359)
C=['yellow','orange','red','purple','blue']
NormActin=minmaxglobal(Actinvalues)
for i in range(0,5):
radii = NormActin[i] #10*np.random.rand(N)
#print(len(radii))
width = np.pi/359.0 #np.pi/4*np.random.rand(N)
bars = ax.bar(theta, radii, width=width, bottom=0.0)
for r,bar in zip(radii, bars):
bar.set_facecolor(C[i])
bar.set_alpha(1.0)

actinFinal=[]
myosinFinal=[]
D=SimData[4]
for i in range(0,COMPARTMENTS):
actinFinal.append(D['Actin'+str(i)][-1])
myosinFinal.append(D['Myosin'+str(i)][-1])
VALS=[]
VALS.append(myosinFinal)
VALS.append(actinFinal)
f=figure(figsize=(8,8))
ax=f.add_axes([0.1, 0.1, 0.8, 0.8],polar=True)
theta = np.linspace(0.0, 2.0*np.pi, 359)
C=['red','blue']
for i in range(0,len(VALS)):
radii = VALS[i]
width = np.pi/359.0
bars = ax.bar(theta, radii, width=width, bottom=0.0)
for r,bar in zip(radii, bars):
bar.set_facecolor(C[i])
bar.set_alpha(1.0)

import pickle
f=open('./simulationdata.dat','w')
pickle.dump(SimData,f)
Plot final network configurations for different $\beta$ values
f, ax = plt.subplots(1,5, subplot_kw=dict(projection='polar'),figsize=(20,5))
for fig in range(0,5):
actinFinal=[]
myosinFinal=[]
D=SimData[fig]
for i in range(0,COMPARTMENTS):
actinFinal.append(D['Actin'+str(i)][-1])
myosinFinal.append(D['Myosin'+str(i)][-1])
VALS=[]
VALS.append(actinFinal)
VALS.append(myosinFinal)
theta = np.linspace(0.0, 2.0*np.pi, 359)
C=['red','blue']
for i in range(0,len(VALS)):
radii = VALS[i]
width = np.pi/359.0
bars = ax[fig].bar(theta, radii, width=width, bottom=0.0)
for r,bar in zip(radii, bars):
bar.set_facecolor(C[i])
bar.set_alpha(1.0)
ax[fig].set_title('$\\beta$= %0.3f'%beta[fig])
plt.savefig('./cytoskeletal-network-rewiring.png')

Generate animations
COMPARTMENTS=359
data=[]
data.append(SimData[0])
data.append(SimData[5])
B=['0.000','0.012']
for t in tqdm(range(0,20)):
f, ax = plt.subplots(1,2, subplot_kw=dict(projection='polar'),figsize=(10,5))
for fig in range(0,2):
actinFinal=[]
myosinFinal=[]
for i in range(0,COMPARTMENTS):
actinFinal.append(data[fig]['Actin'+str(i)][t])
myosinFinal.append(data[fig]['Myosin'+str(i)][t])
VALS=[]
VALS.append(actinFinal)
VALS.append(myosinFinal)
theta = np.linspace(0.0, 2.0*np.pi, 359)
C=['red','blue']
for i in range(0,len(VALS)):
radii = VALS[i]
width = np.pi/359.0
bars = ax[fig].bar(theta, radii, width=width, bottom=0.0)
for r,bar in zip(radii, bars):
bar.set_facecolor(C[i])
bar.set_alpha(1.0)
ax[fig].set_title('$\\beta$='+B[fig])
plt.savefig('./polarization-timecourse-t='+str(t)+'.png')
Generates Ligand distribution plots
S=[0.1,0.5,1.1]
M=[0.5,1.0,1.5]
S.reverse()
M.reverse()
f, ax = plt.subplots(1,2, subplot_kw=dict(projection='polar'),figsize=(10,5))
theta = np.linspace(0.0, 2.0*np.pi, 359)
width = np.pi/359.0
C=['#c0c0c0','#989898','#383838']
#C=['#DAECF3','#022D41','#1AA687']
#C=['#616536','#A4E666','#31B96E']
#C=['red','purple','blue']
i=0
for s in S:
radii=initialLdist(358,1.5,s)
bars = ax[0].bar(theta, radii, width=width, bottom=0.5,edgecolor=C[i])
for r,bar in zip(radii, bars):
bar.set_facecolor(C[i])
bar.set_alpha(1.0)
i=i+1
i=0
for m in M:
radii=initialLdist(358,m,0.75)
bars = ax[1].bar(theta, radii, width=width, bottom=0.5,edgecolor=C[i])
for r,bar in zip(radii, bars):
bar.set_facecolor(C[i])
bar.set_alpha(1.0)
i=i+1
ax[0].get_xaxis().set_visible(False)
ax[0].get_yaxis().set_visible(False)
ax[0].set_title('Depth of Gradient')
ax[1].get_xaxis().set_visible(False)
ax[1].get_yaxis().set_visible(False)
ax[1].set_title('Perceived Ligand gradient')
#plt.savefig('./ligand-distribution.png',dpi=500)

Generates consolidate heatmap collection of all variables with no rewiring
f=open('simulationdata.dat')
SimDat=pickle.load(f)
PTS=SimDat[0]
def makeheatmap(pointset):
COMPARTMENTS=358
pts=pointset
col=[]
mat=[]
HEATMAPS=[]
mat=[]
LVALS=[]
for i in range(0,len(pts['t'])):
LVALS.append(initialLdist(358,1.5,0.75))
HEATMAPS.append(LVALS)
VARIABLES=['Actin','Myosin','PIP','RacGTP','RhoA']
for string in VARIABLES:
mat=[]
col=[]
for j in range(0,len(pts[string+'0'])):
for i in range(0, COMPARTMENTS):
col.append(pts[string+str(i)][j])
mat.append(col)
col=[]
mat.reverse()
HEATMAPS.append(mat)
fig,ax=plt.subplots(2,3,figsize=[15,8],sharex=True, sharey=True)
k=0
print(len(HEATMAPS))
NAMES=['Ligand(input)','Actin','Myosin','PIP','RacGTP','RhoA']
fig.text(0.5, 0.05, 'Compartments', ha='center', va='center')
fig.text(0.1, 0.5, 'Time', ha='center', va='center', rotation='vertical')
for i in range(0,len(ax)):
for j in range(0,len(ax[i])):
ax[i][j].get_yaxis().set_visible(False)
ax[i][j].get_xaxis().set_visible(False)
ax[i][j].set_title(NAMES[k])
sns.heatmap(HEATMAPS[k],ax=ax[i][j],cmap="YlGnBu")
k=k+1
makeheatmap(PTS)
plt.savefig('./representative-results-compilation.png',dpi=500)
6

Comparing strengths of ligand distribution
beta=[0.0]
A={}
graph=rewire(G.copy(),beta)
A=generate_adlist(graph)
COMPARTMENTS=N-1
RevisedCompArgs=dst.args(name='small-world-cyto',
varspecs={
# input set to constant initial value by default
'L[i]':'for(i,0,'+str(COMPARTMENTS)+',0)',#kp-klr*L[i]*R[i]-kd)',
'PIP[i]':'for(i,0,'+str(COMPARTMENTS)+',gamma_pip*(shs(S,wlr*L[i]*R[i]-wpip)-PIP[i]))',
# Regulators
'RacGTP[i]':"for(i,0,"+str(COMPARTMENTS)+",shs(S,-w_rac_rac*RacGTP[i]+w_rac_pip*PIP[i])-RacGTP[i])",
'RhoA[i]':"for(i,0,"+str(COMPARTMENTS)+",(shs(S,wlr_rho*L[i]*R[i]-w_actin_rho*Actin[i])-RhoA[i]))",
},
pars={
# PIP Parameters
'wpip':0.45,
'gamma_pip':0.5,
'wlr':1.0,
# RacGTP activation
'w_rac_pip':3.0,
# Rac
'w_rac_rac':1.5,
# Rho
'w_actin_rho':6.0,
'wlr_rho':1.0,
'S':10,
'kactin':1.0,#0.1,
'w_actin':0.77,
'k_actin_degr':1.0,
'gamma_actin':10.0,
'kmyosin':1.0,
'k_degr_myosin':10
},
ics={
},
fnspecs={
'shs':(['sig','summ'],'1.0/(1.0+exp(-sig*summ))'),
'actinweight':(['n','denom'],'n/denom')
},
tdata=[0,20]
)
SimData=[]
act=[]
RevisedCompArgs.varspecs.update(actindefinition(A))
RevisedCompArgs.varspecs.update(myosindefinition(A))
# RevisedCompArgs.varspecs.update(actindefinition(B))
# RevisedCompArgs.varspecs.update(myosindefinition(B))
S=[0.01,0.1,0.2,0.3,0.4,0.5,0.55,0.6,0.7,0.8,0.9,1.0]
#s=[0.5]
AMRatio=[]
#for v in s:
for s in tqdm(S):
L=initialLdist(COMPARTMENTS,1.5,s)
Rinitial=1.0
PIPinitial=0.0
Racinitial=0.0
Actininital=0.0
Rhoinitial=0.0
Myosininitial=0.0
for i in range(0,COMPARTMENTS+1):
R=str('R'+str(i))
RevisedCompArgs.pars[R]=Rinitial
PIP=str('PIP'+str(i))
RevisedCompArgs.ics[PIP]=PIPinitial
Rac=str('RacGTP'+str(i))
RevisedCompArgs.ics[Rac]=Racinitial
Actin=str('Actin'+str(i))
RevisedCompArgs.ics[Actin]=Actininital
Rho=str('RhoA'+str(i))
RevisedCompArgs.ics[Rho]=Rhoinitial
Myosin=str('Myosin'+str(i))
RevisedCompArgs.ics[Myosin]=Myosininitial
Lval=str('L'+str(i))
RevisedCompArgs.ics[Lval]=L[i]
RevisedCompDS=dst.Vode_ODEsystem(RevisedCompArgs)
pts=RevisedCompDS.compute('test').sample(dt=0.5)
ratioVals=[]
for j in range(0,COMPARTMENTS+1):
ratioVals.append(pts['Actin'+str(j)][-1]/pts['Myosin'+str(j)][-1])
AMRatio.append(ratioVals)
def minmaxnorm(A):
MI=min(A)
MA=max(A)
B=[]
for a in A:
B.append((a-MI)/(MA-MI))
return B
mag=[]
for i in range(0,len(AMRatio)):
re=0
im=0
for j in range(0,len(AMRatio[0])):
re=re+AMRatio[i][j]*np.cos(np.pi/180.0*j)
im=im+AMRatio[i][j]*np.sin(np.pi/180.0*j)
mag.append(np.sqrt(re**2+im**2))
plt.plot(S,minmaxnorm(mag))
plt.xlabel('Standard Deviation | Steepness of Gradient')
plt.ylabel('Actin:Myosin Ratio | Polarization')
plt.savefig('chemotaxis-phenotype-ligand-input.png',dpi=500)
# mag1=[]
# for s in S:
# L=initialLdist(COMPARTMENTS,1.5,s)
# for i in range(0,len(L)):
# re=re+L[i]*np.cos(np.pi/180.0*i)
# im=im+L[i]*np.sin(np.pi/180.0*i)
# mag1.append(np.sqrt(re**2+im**2))
# plt.plot(S,minmaxnorm(mag1),'r')

Effect of network randomization
beta=[0.0,0.012]
Adict=[]
for b in beta:
A={}
graph=rewire(G.copy(),beta)
A=generate_adlist(graph)
Adict.append(A)
COMPARTMENTS=N-1
RevisedCompArgs=dst.args(name='small-world-cyto',
varspecs={
# input set to constant initial value by default
'L[i]':'for(i,0,'+str(COMPARTMENTS)+',0)',#kp-klr*L[i]*R[i]-kd)',
'PIP[i]':'for(i,0,'+str(COMPARTMENTS)+',gamma_pip*(shs(S,wlr*L[i]*R[i]-wpip)-PIP[i]))',
# Regulators
'RacGTP[i]':"for(i,0,"+str(COMPARTMENTS)+",shs(S,-w_rac_rac*RacGTP[i]+w_rac_pip*PIP[i])-RacGTP[i])",
'RhoA[i]':"for(i,0,"+str(COMPARTMENTS)+",(shs(S,wlr_rho*L[i]*R[i]-w_actin_rho*Actin[i])-RhoA[i]))",
},
pars={
# PIP Parameters
'wpip':0.45,
'gamma_pip':0.5,
'wlr':1.0,
# RacGTP activation
'w_rac_pip':3.0,
# Rac
'w_rac_rac':1.5,
# Rho
'w_actin_rho':6.0,
'wlr_rho':1.0,
'S':10,
'kactin':1.0,#0.1,
'w_actin':0.77,
'k_actin_degr':1.0,
'gamma_actin':10.0,
'kmyosin':1.0,
'k_degr_myosin':10
},
ics={
},
fnspecs={
'shs':(['sig','summ'],'1.0/(1.0+exp(-sig*summ))'),
'actinweight':(['n','denom'],'n/denom')
},
tdata=[0,20]
)
SimData=[]
act=[]
# RevisedCompArgs.varspecs.update(actindefinition(B))
# RevisedCompArgs.varspecs.update(myosindefinition(B))
S=[0.01,0.1,0.2,0.3,0.4,0.5,0.55,0.6,0.7,0.8,0.9,1.0]
#s=[0.5]
ValueList=[]
for A in Adict:
AMRatio=[]
RevisedCompArgs.varspecs.update(actindefinition(A))
RevisedCompArgs.varspecs.update(myosindefinition(A))
#for v in s:
for s in tqdm(S):
L=initialLdist(COMPARTMENTS,1.5,s)
Rinitial=1.0
PIPinitial=0.0
Racinitial=0.0
Actininital=0.0
Rhoinitial=0.0
Myosininitial=0.0
for i in range(0,COMPARTMENTS+1):
R=str('R'+str(i))
RevisedCompArgs.pars[R]=Rinitial
PIP=str('PIP'+str(i))
RevisedCompArgs.ics[PIP]=PIPinitial
Rac=str('RacGTP'+str(i))
RevisedCompArgs.ics[Rac]=Racinitial
Actin=str('Actin'+str(i))
RevisedCompArgs.ics[Actin]=Actininital
Rho=str('RhoA'+str(i))
RevisedCompArgs.ics[Rho]=Rhoinitial
Myosin=str('Myosin'+str(i))
RevisedCompArgs.ics[Myosin]=Myosininitial
Lval=str('L'+str(i))
RevisedCompArgs.ics[Lval]=L[i]
RevisedCompDS=dst.Vode_ODEsystem(RevisedCompArgs)
pts=RevisedCompDS.compute('test').sample(dt=0.5)
ratioVals=[]
for j in range(0,COMPARTMENTS+1):
ratioVals.append(pts['Actin'+str(j)][-1]/pts['Myosin'+str(j)][-1])
AMRatio.append(ratioVals)
ValueList.append(AMRatio)
k=0
lab=['Wt','Noc']
for AMRatio in ValueList:
mag=[]
for i in range(0,len(AMRatio)):
re=0
im=0
for j in range(0,len(AMRatio[0])):
re=re+AMRatio[i][j]*np.cos(np.pi/180.0*j)
im=im+AMRatio[i][j]*np.sin(np.pi/180.0*j)
mag.append(np.sqrt(re**2+im**2))
plt.plot(S,minmaxnorm(mag),label=lab[k])
k=k+1
plt.legend()
plt.xlabel('Standard Deviation | Steepness of Gradient')
plt.ylabel('Actin:Myosin Ratio | Polarization')
plt.savefig('rewiring-comparison.png',dpi=500)

No statistical difference observable. This will be more meaningful with more random networks maybe?



